
Assignment 4
Centers of a Triangle
Nicolina Scarpelli
Introduction
In this assignment we are going to explore the centers of a triangle and review basic concepts of triangle geometry. These explorations can be very engaging especially to students in a high school geometry class. As teachers we need to make learning interactive, and by using Geometer's Sketchpad you can show the students important steps and concepts in understanding the difference between the centers of a triangle.
Let's begin this exploration by using Geometer's Sketchpad to construct the Centroid of a triangle. The centroid of a triangle is the common intersection of the three medians. A median of a triangle is the segment from a vertex to the midpoint of the opposite side. The location of the centroid of a triangle will change with various shapes of triangles.
Let's begin by constructing three points. Then connect those three points by constructing segments, and a triangle is obtained. Construct the midpoints of each of these three segments. Then construct the three medians of a triangle, the segment from the vertex to the midpoint of the opposite side. Where the three medians are concurrent is the centroid.
Click here for the GSP construction of a centroid.
Use the GSP construction and you can move the vertices of the triangle to make a newly shaped triangle. Notice that no matter what shape your triangle is, the centroid will always be located inside the triangle. For many purposes in physics and mechanics, it is necessary or useful to be able to consider a physical object as being a mass concentrated at a single point, its geometric center, the centroid. In physics, the centroid is the center of mass and is essentially the "average" of all the points in the object.
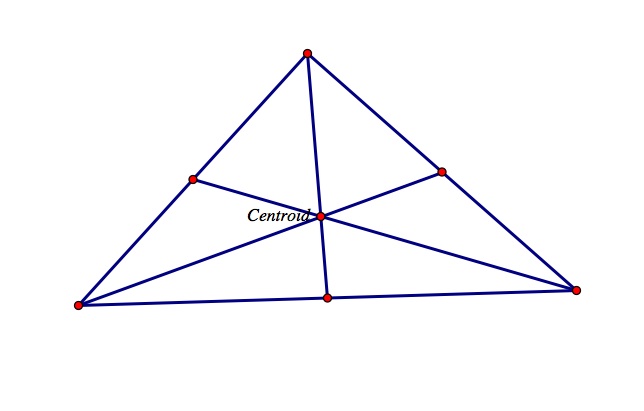
Investigation 1: Observe the triangle below. The point labeled G is the centroid.
Here,
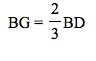
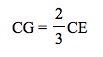
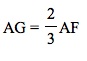
Why do these equations hold? Let's prove the three medians of a triangle are concurrent and the centroid is (2/3) the distance from a vertex to the midpoint of the opposite side.
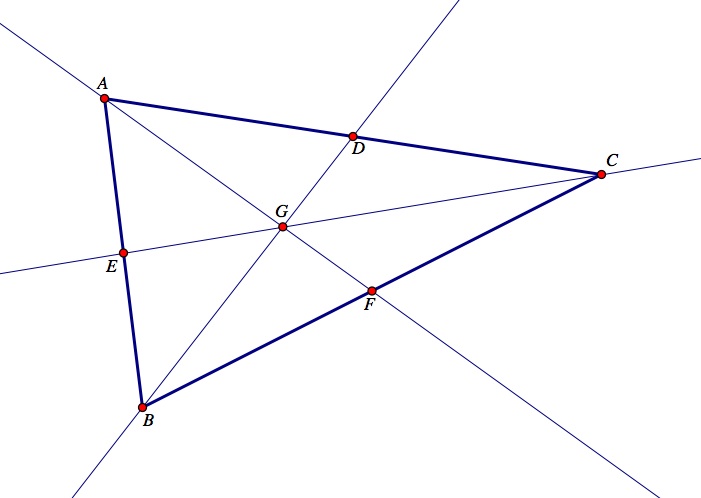
Let's begin by proving the concurrency of the medians. In order to prove concurrency of the medians, let's start by constructing D to be the midpoint of the segment AC and E to be the midpoint of the segment AB. Then, construct the segments BD and CE. Let their intersection point be labeled G. Then construct the segment DE.
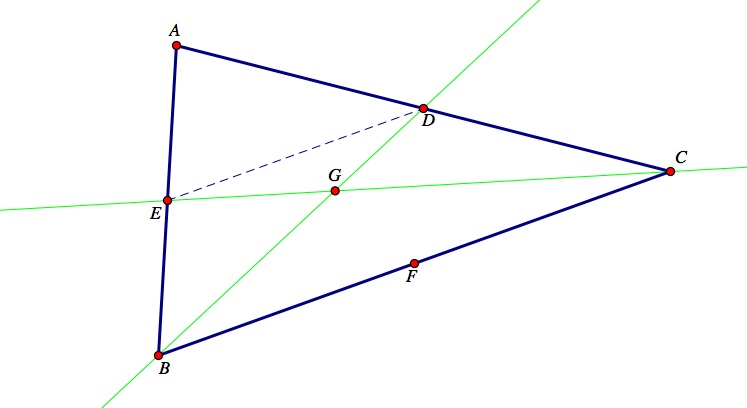
Notice that the segment DE is the mid-segment of triangle ABC. The mid-segment DE is parallel to the side BC and the length of DE is equal to 1/2 of the length of BC or 2DE = BC.
Next, using the alternate interior angles theorem we can prove angle ∠DEG ≅ angle ∠GCB, and angle ∠EDG ≅ ∠GBC. Since two angles are congruent in the triangle EDG and triangle CBG we can use the Angle-Angle postulate to prove that the two triangles are in fact similar triangles. Observe the blue triangle is similar to the pink triangle in the sketch below.
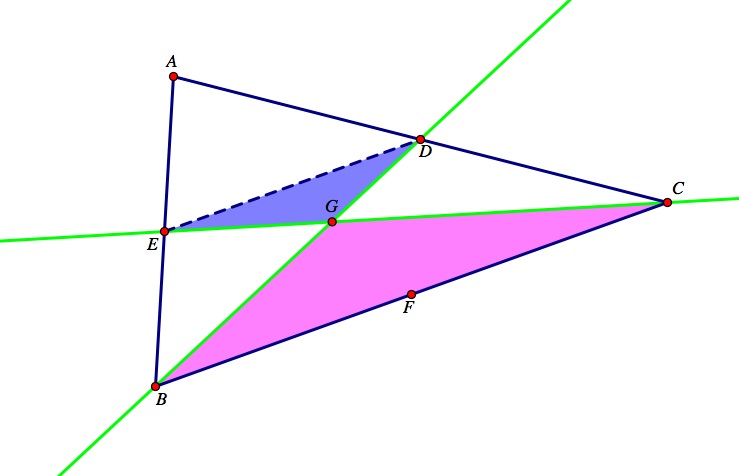
Since the triangles are similar, this implies that the sides of the two triangles are proportional. Thus,
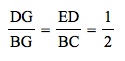
Solving the proportion gives us 2DG = BG. Therefore,
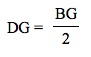
So if you split BG into two parts (each part being equal to length DG) then you will have split the whole segment BD into three equal parts (each part being equal to length DG). Thus,
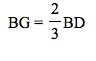
and
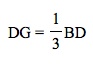
Similarly,
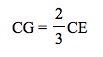
and
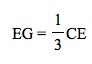
Observe the sketch below.
proof.jpg)
Therefore, the median CE bisects the median BD at a point that is two thirds of the way from B to D. Median BD bisects median CE at a point that is two-thirds of the way from C to E, and if we were to construct a median from A to a point F then the median from A to F will also cut BD at a point that is two-thirds of the way from B to D, and will intersect the centroid, G. Therefore, the three medians in a triangle must meet at a point, thus be concurrent at a point G, and this point is exactly two- thirds the distance from each vertex to the midpoint of the opposite sides. Click here for a GSP file.
Investigation 2: The medians divide the triangle into six small triangles. Show that these triangles all have the same area.
Using GSP and the constructed triangle from above, we can see that the triangle ABC is divided into 6 triangles with each triangle having the same area. Observe the GSP file here.
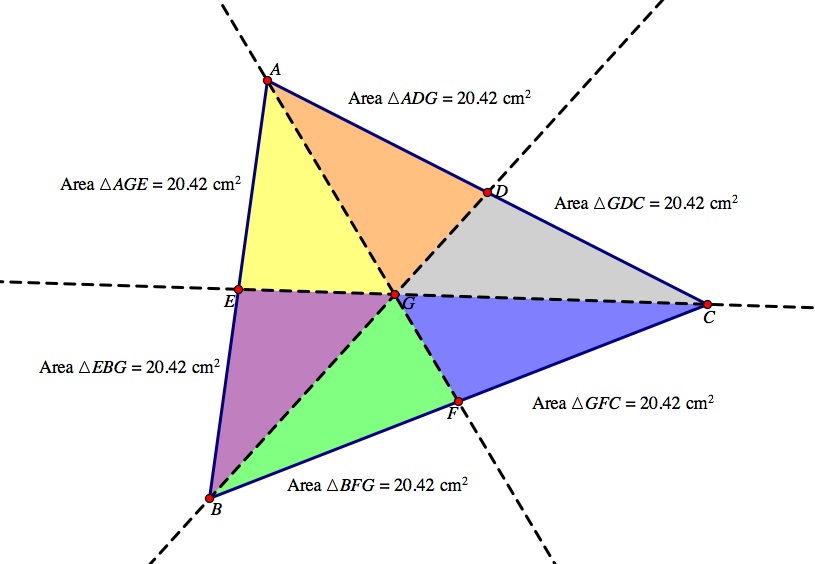
What is really cool about this construction is that even though these are not congruent triangles necessarily, all 6 of the triangles have the same area. Let's begin by looking at different pairs of triangles. Take the two triangles, triangle BFG and the triangle GFC. Notice that they have the same altitude because they share the same vertex. They also have the same height and same base BC. Therefore, the length of BF = the length of FC. Since Area = (1/2)(base)(height) the two triangles BFG and GFC will have the same area because they have the same height and base. How would you go about proving the rest of the triangles have the same area? We will use the exact same logic for the rest of the triangles. We will divide the triangles into three pairs. Let the area of triangle BFG and the area of triangle GFC = y
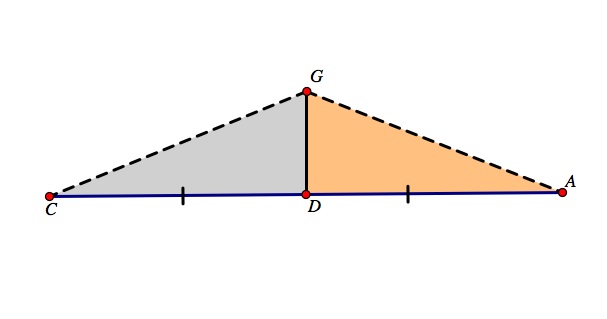
Take the next two triangles CGD and AGD. Notice once again, the two triangles share the same base AC, and the length of CD = length of AD. In addition, the two triangles share the same height. Thus, by the same logic, the area of triangle CGD is equal to the triangle of AGD. Let the area of triangle CGD and the area of triangle AGD = x
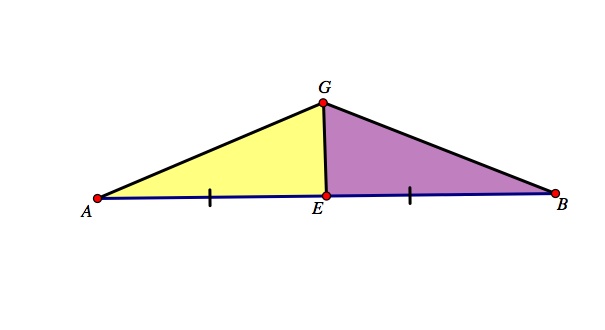
Taking the next two triangles, AGE and BGE, we can apply the same concept. Thus they have the same height and same base so their areas are equal. Let the area of triangle AGE and triangle BGE = z.
Now we have the six triangles with area labeled as such.
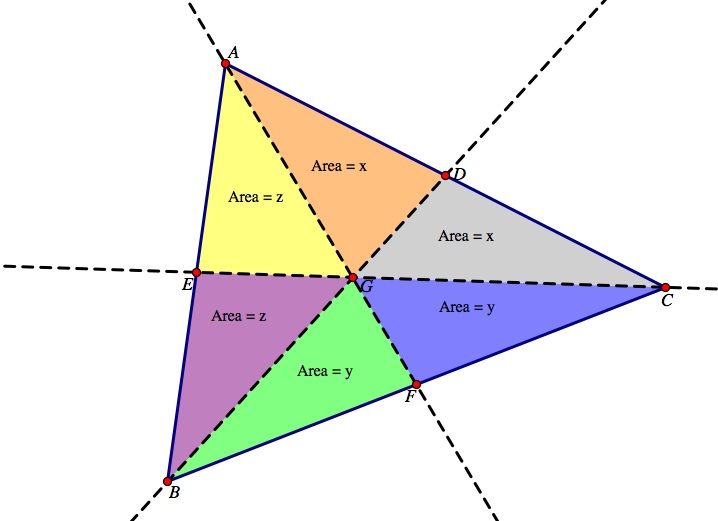
Now, we want to split the triangles up again and find the area of triangle ABF (outlined in red) and find the area of triangle ACF (outlined in blue). They share a common side shown in black. 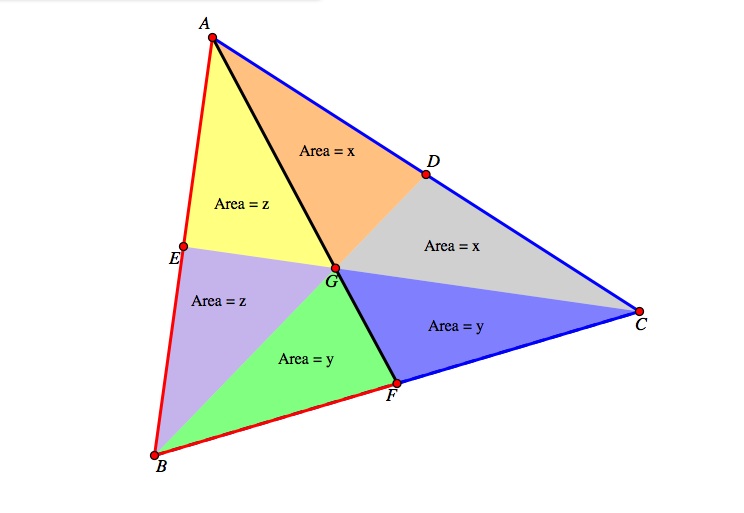
The areas of those two triangles will equal each other as well. Thus x + x + y = z + z + y. Simplifying this equation gives up 2x + y = 2z + y, thus leading to x = z. So now we have 4 triangles with the area of x, and have to prove the two other triangles are also equal to area x.
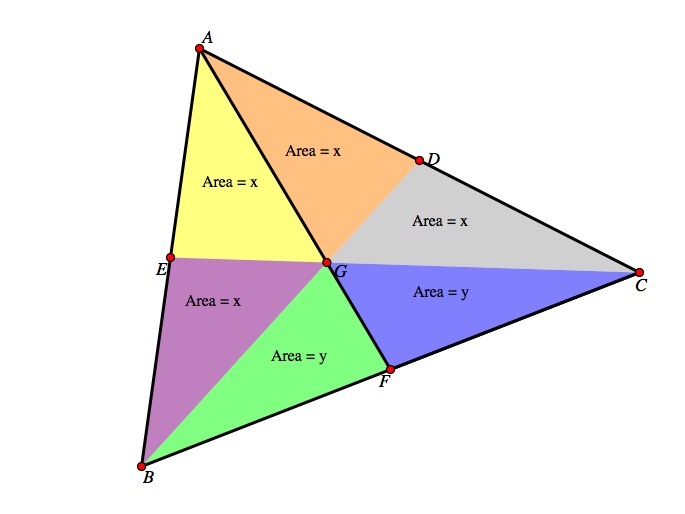
Now we will look at triangle BDC (outlined in pink) and triangle BDA(outlined in light blue). They share a common side (shown in black). We will continue the process as worked in the above exercises.
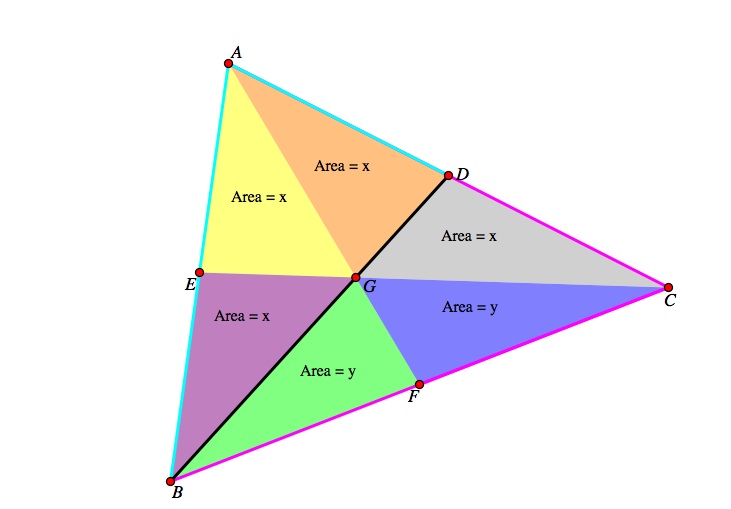
The area of triangle BDC is x + y + y and the area of triangle BDA is x + x + x = 3x. We can set these areas equal to each other because triangle BDC and triangle BDA have the same base and the same height. We are just invoking the same principle over and over again. Thus, setting those areas equal to each other: 2x + y = 3x which simplifies to 2x = 2y thus y = x.
Therefore, each of the six triangles has an area equal to x.
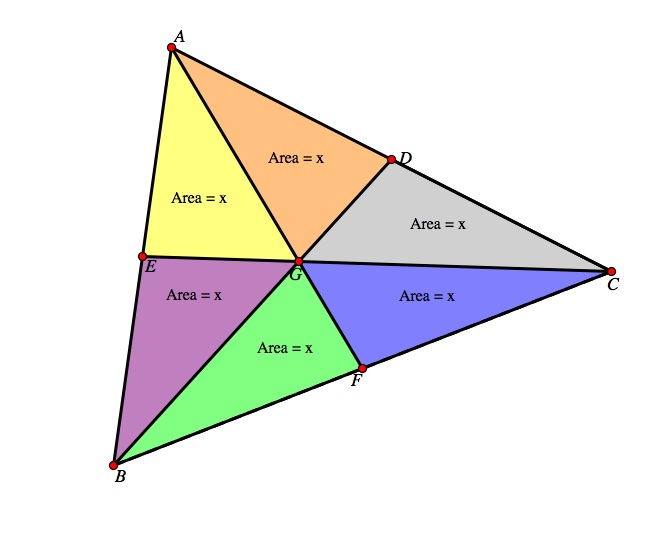
Thus, the medians divide the triangle into six small triangles, and these triangles all have the same area.
Next, let's construct the Orthocenter of a triangle. The orthocenter of a triangle is the point of concurrency or the common intersection of the three lines containing the altitudes. An altitude is a perpendicular segment from a vertex to the line of the opposite side.
Use Geometer's Sketchpad to create the orthocenter of a triangle. Begin by constructing a triangle, as done for the construction of the centroid. Then, construct the three altitudes of the triangle. The altitudes of the triangle are the perpendicular segments from the vertex to the line of the opposite side. The concurrency of three of the altitudes is the orthocenter, label this point of concurrency "orthocenter".
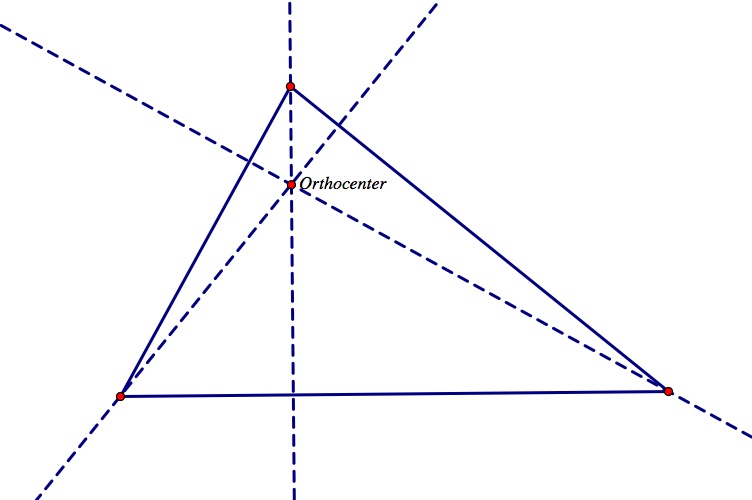
For a GSP construction of an orthocenter click here
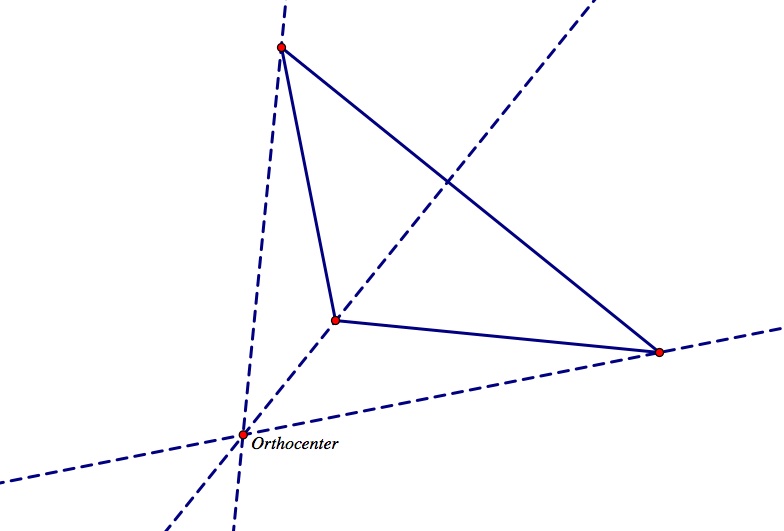
Notice if you move the vertices of the triangle, the orthocenter moves as well; thus, the orthocenter is not always inside the triangle like the centroid. If the triangle is obtuse, the orthocenter will be outside of the triangle opposite to the longest leg on the same side as the largest angle. This is shown below. Notice also, that in a right triangle, the orthocenter falls on a vertex of the triangle.
Next, let's construct the Circumcenter of a triangle. The Circumcenter of a triangle is the point in the plane equidistant from the three vertices of the triangle. The circumcenter forms the origin of a circle in which all three vertices of the triangle lie on the circle. We will use Geometer's Sketchpad to construct the circumcenter of a triangle.
Begin by constructing a triangle. Then, construct the midpoints of each of the segments(legs of the triangle). Then construct perpendicular bisectors of the triangle, which are the lines perpendicular to the sides of a triangle through the midpoints of the side. In order to do this, select the midpoint and then select the side of the triangle and then go to the construct drop down menu and click perpendicular line. The point of concurrency of three of the perpendicular bisectors will be the circumcenter. Observe the sketch below.
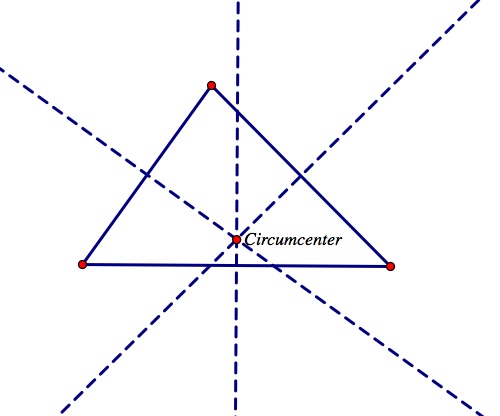
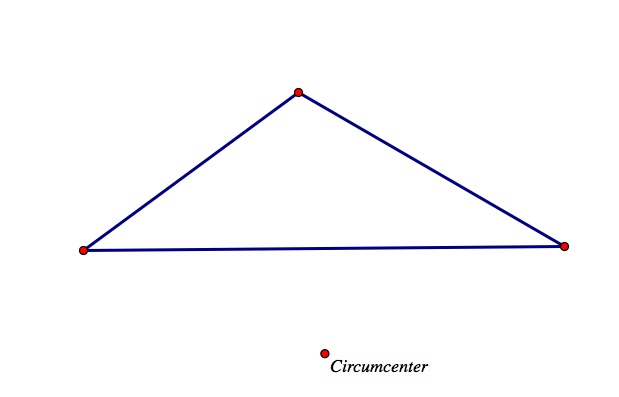
The circumcenter is not always located inside the triangle. Just like the orthocenter, it can be located outside the triangle as well. See the sketch below.
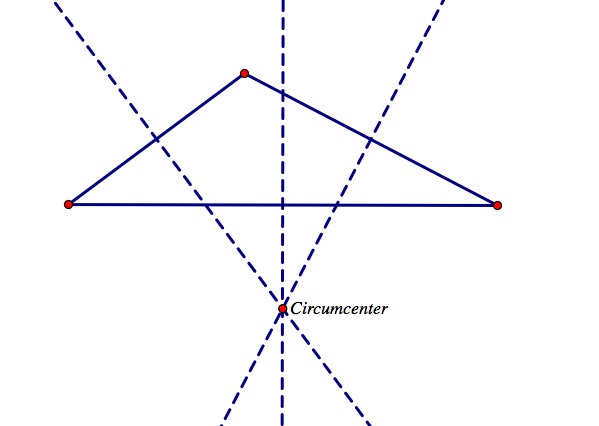
Click here for a GSP construction of a circumcenter. Move the vertices of the triangle to make different triangle shapes and notice the location of the circumcenter. Try making a right triangle, where is the circumcenter located? Observe many different obtuse triangles. Notice the circumcenter is always outside the triangle and located on the opposite side of the largest angle of the triangle. Observe the sketch below.
The final GSP construction we will create is the Incenter of a triangle. The incenter of a triangle is the point on the interior of the triangle that is equidistant from the three sides. The incenter is constructed by taking the intersection of the angle bisectors of the three vertices of the triangle.
Let's begin by constructing a triangle. Then construct the three angle bisectors of the angles of the triangle. Do this by clicking on a vertex, and the two sides forming the vertex selected, go to the construct menu and click angle bisector. The point of concurrency of three of the angle bisectors is the incenter of the triangle, label this point, "incenter".
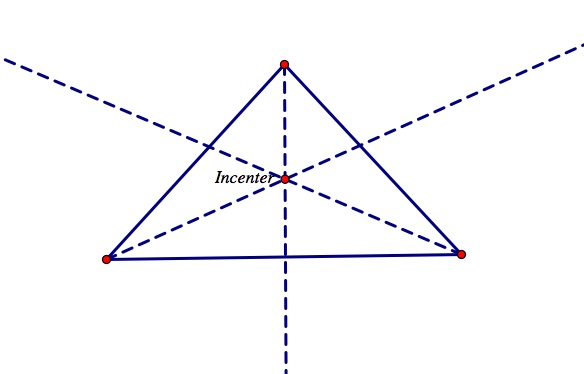
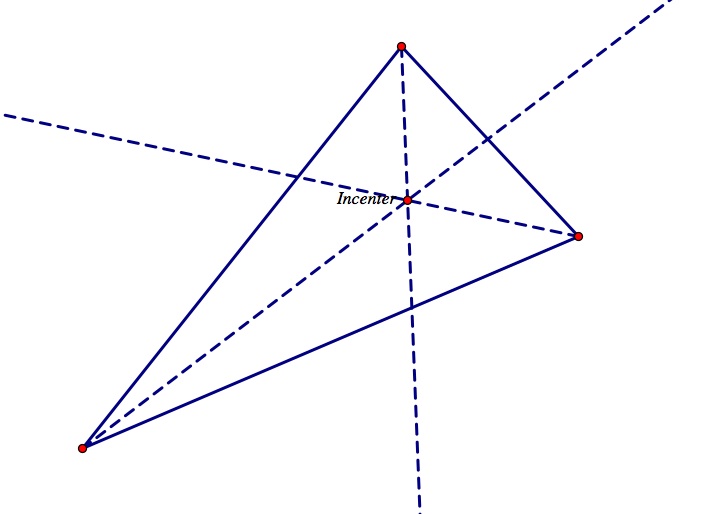
Click here for a GSP construction of the incenter. Notice that the incenter is always located inside the triangle just like the centroid. See the obtuse triangle below. In addition, if you move the vertices of the triangle in the GSP construction, you can see that no matter what shape of triangle you create, the incenter will always be located inside.
Is there any relationship between the orthocenter, incenter, and circumcenter of a triangle? Observe the sketch below where the orthocenter, centroid, and circumcenter are all created for the same triangle.
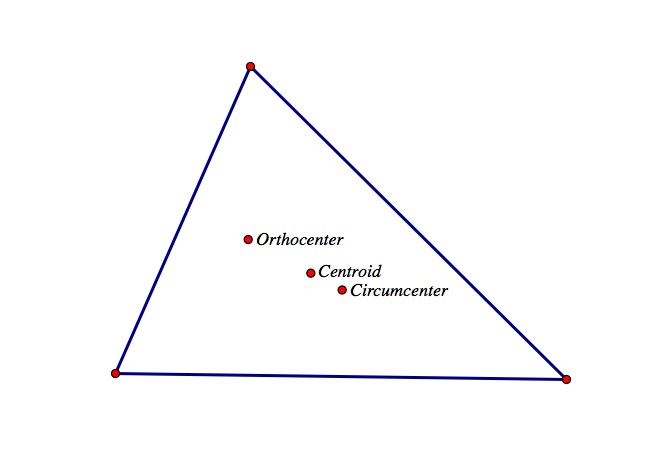
What do you see? Do you notice the three points form a straight line?
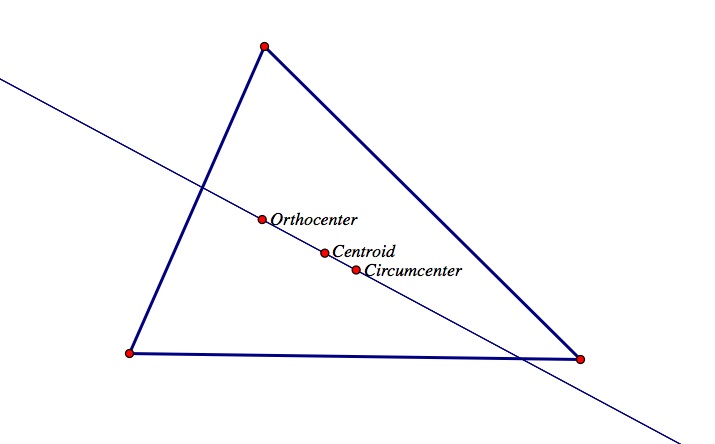
This is an interesting characteristic of the orthocenter, centroid, and circumcenter of a triangle. They, in fact, do form a straight line. In addition, the distance between the orthocenter and the centroid is always twice the distance between the centroid and the circumcenter. Notice below that the distance from the orthocenter to the centroid is equal to 2.508 which is twice the distance from the centroid to the circumcenter which is 1.254.
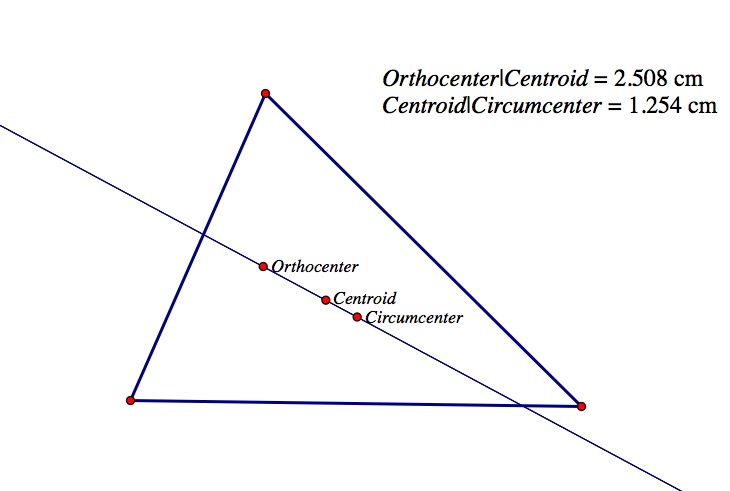
Click here to observe the GSP construction that plots the orthocenter, centroid, and circumcenter of the same triangle.
Will the orthocenter, the circumcenter, and the centroid ever be the same point in a triangle? If so, what type of triangle will you have to have for this to happen? Will the incenter ever be in the same place as the other three points? Is there a special relationship between the incenter and the other three centers?
Return to Home Page



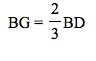
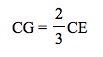
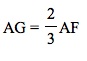


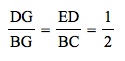
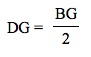
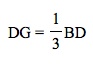
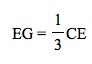
proof.jpg)

















